An example when unimodal nonnegative is better than point exponential prior
DongyueXie
2023-02-09
Last updated: 2023-02-09
Checks: 7 0
Knit directory: gsmash/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20220606) was run prior to running
the code in the R Markdown file. Setting a seed ensures that any results
that rely on randomness, e.g. subsampling or permutations, are
reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 3638ec1. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for
the analysis have been committed to Git prior to generating the results
(you can use wflow_publish or
wflow_git_commit). workflowr only checks the R Markdown
file, but you know if there are other scripts or data files that it
depends on. Below is the status of the Git repository when the results
were generated:
Ignored files:
Ignored: .Rhistory
Ignored: .Rproj.user/
Untracked files:
Untracked: analysis/movielens.Rmd
Untracked: analysis/pbmc3k_nonnegLF_updatef0.Rmd
Untracked: analysis/profiled_obj_for_b_splitting.Rmd
Untracked: data/ml-latest-small/
Untracked: output/droplet_iteration_results/
Untracked: output/ebpmf_pbmc3k_vga3_glmpca_init.rds
Untracked: output/pbmc3k_iteration_results/
Untracked: output/pbmc_no_constraint.rds
Unstaged changes:
Modified: analysis/index.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were
made to the R Markdown
(analysis/example_unimodal_nonnegative_better_than_point_exponential.Rmd)
and HTML
(docs/example_unimodal_nonnegative_better_than_point_exponential.html)
files. If you’ve configured a remote Git repository (see
?wflow_git_remote), click on the hyperlinks in the table
below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 3638ec1 | DongyueXie | 2023-02-09 | wflow_publish("analysis/example_unimodal_nonnegative_better_than_point_exponential.Rmd") |
When imposing nonnegative constraint on L and F, there are two
choices of priors in ebnm - unimodal nonnegative, and point
exponential.
Here I show an example where unimodal nonnegative performs better in terms of recovering structure. But point exponential is much faster.
library(stm)set.seed(12345)
N = 1000
p = 100
K = 3
sigma2 = 0.25
Ftrue = matrix(0,nrow=p,ncol=K)
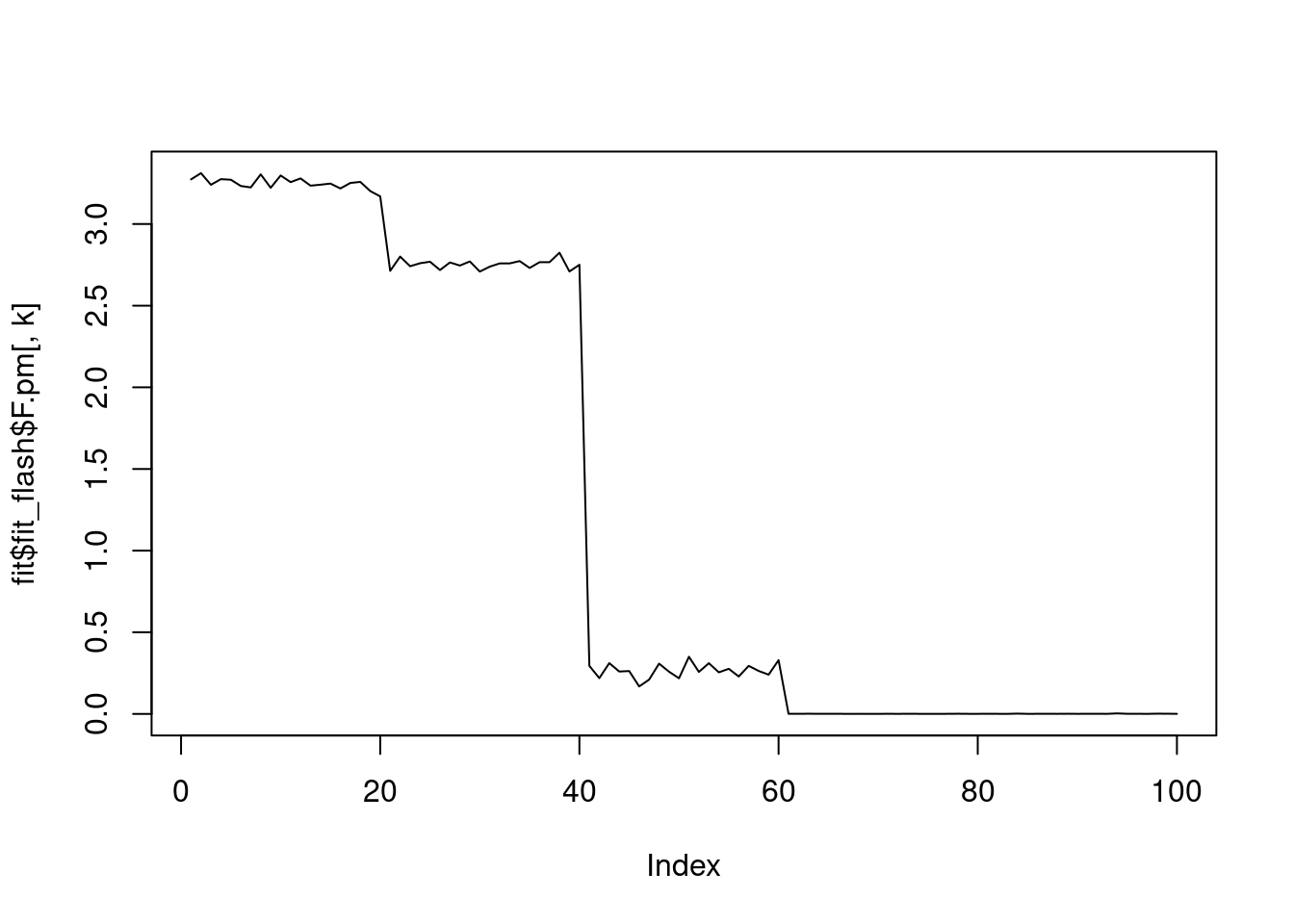
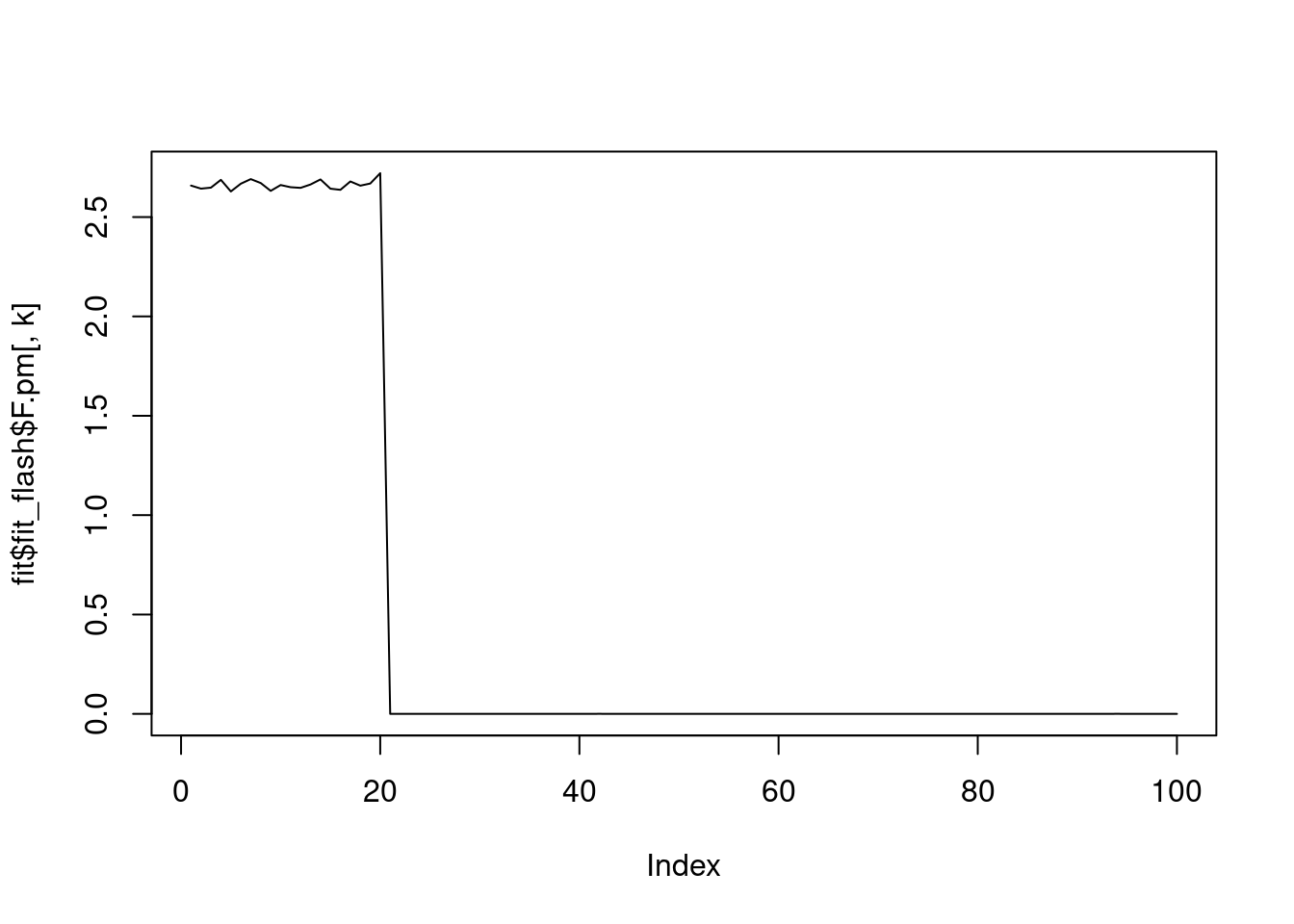
Ftrue[1:20,1] = 3
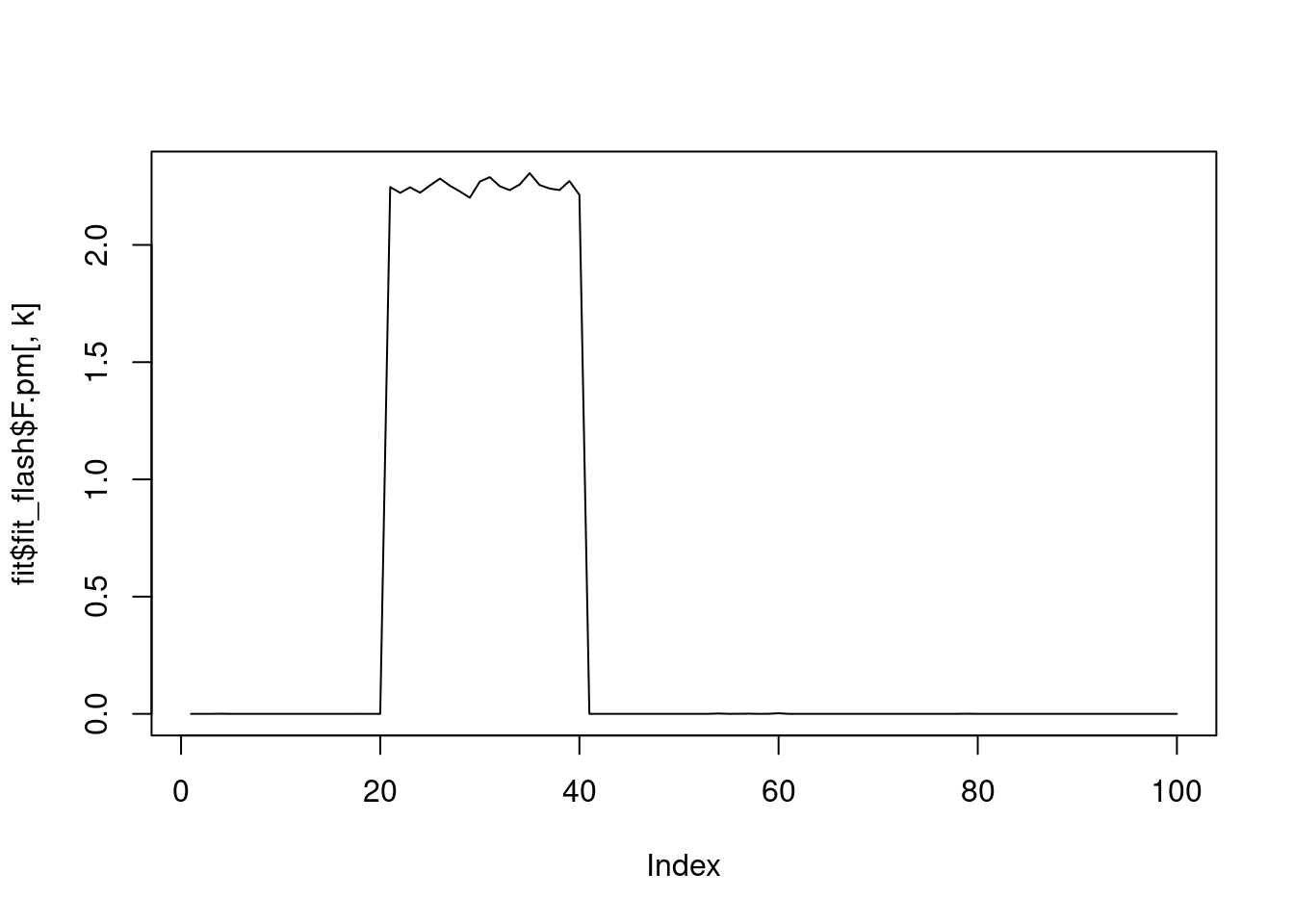
Ftrue[21:40,2] = 2
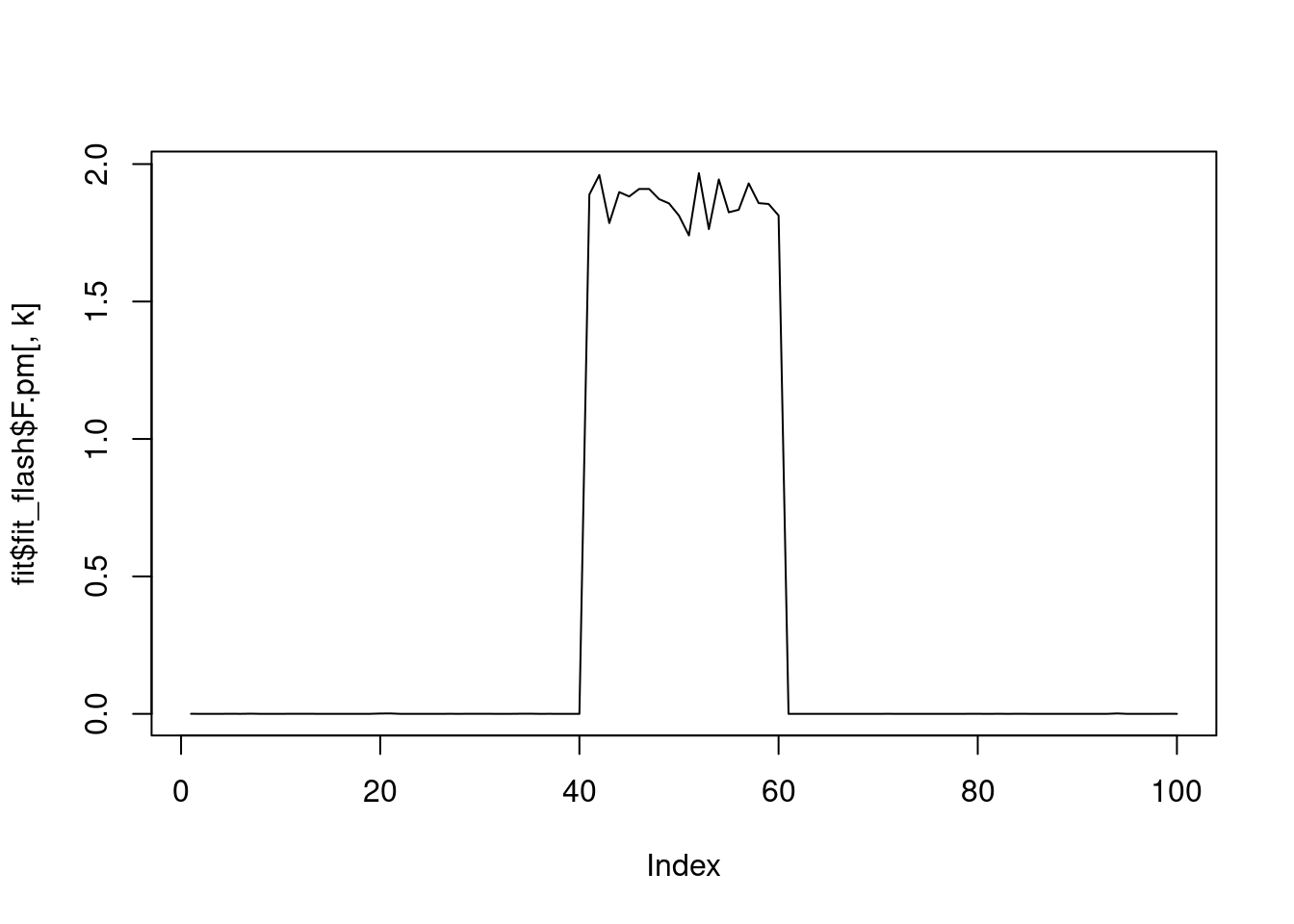
Ftrue[41:60,3] = 1
Ltrue = matrix(rnorm(N*K), ncol=K)point exponential fit
Lambda = exp(tcrossprod(abs(Ltrue),abs(Ftrue))+ matrix(rnorm(N*p,0,sqrt(sigma2)),nrow=N))
Y = matrix(rpois(N*p,Lambda),nrow=N,ncol=p)
fit = ebpmf_log(Y,verbose=TRUE,l0=1,f0=1,est_f0 = F,
ebnm.fn = c(ebnm::ebnm_point_exponential, ebnm::ebnm_point_exponential),
loadings_sign = 1,factors_sign = 1,maxiter = 100,printevery = 1,return_sigma2_trace = T)Initializing M...Solving VGA for column 1...1 ...2 ...3 ...4 ...5 ...6 ...7 ...8 ...9 ...10 ...11 ...12 ...13 ...14 ...15 ...16 ...17 ...18 ...19 ...20 ...21 ...22 ...23 ...24 ...25 ...26 ...27 ...28 ...29 ...30 ...31 ...32 ...33 ...34 ...35 ...36 ...37 ...38 ...39 ...40 ...41 ...42 ...43 ...44 ...45 ...46 ...47 ...48 ...49 ...50 ...51 ...52 ...53 ...54 ...55 ...56 ...57 ...58 ...59 ...60 ...61 ...62 ...63 ...64 ...65 ...66 ...67 ...68 ...69 ...70 ...71 ...72 ...73 ...74 ...75 ...76 ...77 ...78 ...79 ...80 ...81 ...82 ...83 ...84 ...85 ...86 ...87 ...88 ...89 ...90 ...91 ...92 ...93 ...94 ...95 ...96 ...97 ...98 ...99 ...100 ...
running initial flash fit
Running iterations...
iter 1, elbo=-249456.04629, K=3
iter 2, elbo=-240237.19642, K=4
iter 3, elbo=-233476.637, K=4
iter 4, elbo=-230096.02745, K=4
iter 5, elbo=-228369.74169, K=4
--Estimate of factor 5 is numerically zero!
--Estimate of factor 5 is numerically zero!
iter 6, elbo=-227413.64468, K=4
--Estimate of factor 5 is numerically zero!
--Estimate of factor 5 is numerically zero!
iter 7, elbo=-226908.35645, K=4
--Estimate of factor 5 is numerically zero!
--Estimate of factor 5 is numerically zero!
iter 8, elbo=-226611.44983, K=4
iter 9, elbo=-226438.35721, K=5
--Estimate of factor 5 is numerically zero!
--Estimate of factor 5 is numerically zero!
iter 10, elbo=-226329.84149, K=5
iter 11, elbo=-226260.4124, K=6
iter 12, elbo=-226214.3678, K=7
iter 13, elbo=-226183.13017, K=8
iter 14, elbo=-226161.21479, K=9
iter 15, elbo=-226145.3721, K=10
iter 16, elbo=-226133.53182, K=11
iter 17, elbo=-226124.30442, K=12
iter 18, elbo=-226116.86042, K=13
iter 19, elbo=-226110.56894, K=14
iter 20, elbo=-226104.97767, K=15
--Estimate of factor 10 is numerically zero!
--Estimate of factor 10 is numerically zero!
iter 21, elbo=-226099.69183, K=15
--Estimate of factor 9 is numerically zero!
iter 22, elbo=-226095.37783, K=15
iter 23, elbo=-226092.10967, K=16
iter 24, elbo=-226089.46359, K=17
iter 25, elbo=-226087.37294, K=18
iter 26, elbo=-226085.63856, K=19
iter 27, elbo=-226084.18102, K=20
iter 28, elbo=-226082.87433, K=21
iter 29, elbo=-226081.09458, K=22
--Estimate of factor 10 is numerically zero!
--Estimate of factor 10 is numerically zero!for(k in 1:fit$fit_flash$n.factors){
plot(fit$fit_flash$F.pm[,k],type='l')
}
fit$elbo[1] -226080.7plot(fit$fit_flash$pve)
fit$run_timeTime difference of 33.02008 secsunlist(lapply(fit$run_time_break_down,mean)) run_time_vga_init run_time_flash_init
0.25305605 0.53625202
run_time_vga run_time_flash_init_factor
0.03570487 0.03501945
run_time_flash_greedy run_time_flash_backfitting
0.20070823 0.72873402
run_time_flash_nullcheck
0.05960391 unimodal nonnegative
Lambda = exp(tcrossprod(abs(Ltrue),abs(Ftrue))+ matrix(rnorm(N*p,0,sqrt(sigma2)),nrow=N))
Y = matrix(rpois(N*p,Lambda),nrow=N,ncol=p)
fit = ebpmf_log(Y,verbose=TRUE,l0=1,f0=1,est_f0 = F,
ebnm.fn = c(ebnm::ebnm_unimodal_nonnegative, ebnm::ebnm_unimodal_nonnegative),
loadings_sign = 1,factors_sign = 1,maxiter = 100,printevery = 1,return_sigma2_trace = T)Initializing M...Solving VGA for column 1...1 ...2 ...3 ...4 ...5 ...6 ...7 ...8 ...9 ...10 ...11 ...12 ...13 ...14 ...15 ...16 ...17 ...18 ...19 ...20 ...21 ...22 ...23 ...24 ...25 ...26 ...27 ...28 ...29 ...30 ...31 ...32 ...33 ...34 ...35 ...36 ...37 ...38 ...39 ...40 ...41 ...42 ...43 ...44 ...45 ...46 ...47 ...48 ...49 ...50 ...51 ...52 ...53 ...54 ...55 ...56 ...57 ...58 ...59 ...60 ...61 ...62 ...63 ...64 ...65 ...66 ...67 ...68 ...69 ...70 ...71 ...72 ...73 ...74 ...75 ...76 ...77 ...78 ...79 ...80 ...81 ...82 ...83 ...84 ...85 ...86 ...87 ...88 ...89 ...90 ...91 ...92 ...93 ...94 ...95 ...96 ...97 ...98 ...99 ...100 ...
running initial flash fit
Running iterations...
iter 1, elbo=-249763.19499, K=3
iter 2, elbo=-240554.79883, K=4
iter 3, elbo=-233788.22043, K=4
iter 4, elbo=-230402.15789, K=4
iter 5, elbo=-228629.00426, K=4
iter 6, elbo=-227637.72587, K=4
iter 7, elbo=-227103.54606, K=4
iter 8, elbo=-226783.48974, K=4
iter 9, elbo=-226591.68011, K=4
iter 10, elbo=-226468.95583, K=4
iter 11, elbo=-226390.60371, K=4
iter 12, elbo=-226340.54857, K=4
iter 13, elbo=-226306.11576, K=4
iter 14, elbo=-226280.57372, K=4
iter 15, elbo=-226262.43144, K=4
iter 16, elbo=-226249.4214, K=4
iter 17, elbo=-226240.09595, K=4
iter 18, elbo=-226233.20663, K=4
iter 19, elbo=-226227.88184, K=4
iter 20, elbo=-226223.4926, K=4
iter 21, elbo=-226219.5519, K=4
iter 22, elbo=-226216.12748, K=4
iter 23, elbo=-226213.32169, K=4
iter 24, elbo=-226211.0799, K=4
iter 25, elbo=-226209.29097, K=4
iter 26, elbo=-226207.83113, K=4
iter 27, elbo=-226206.63343, K=4for(k in 1:fit$fit_flash$n.factors){
plot(fit$fit_flash$F.pm[,k],type='l')
}
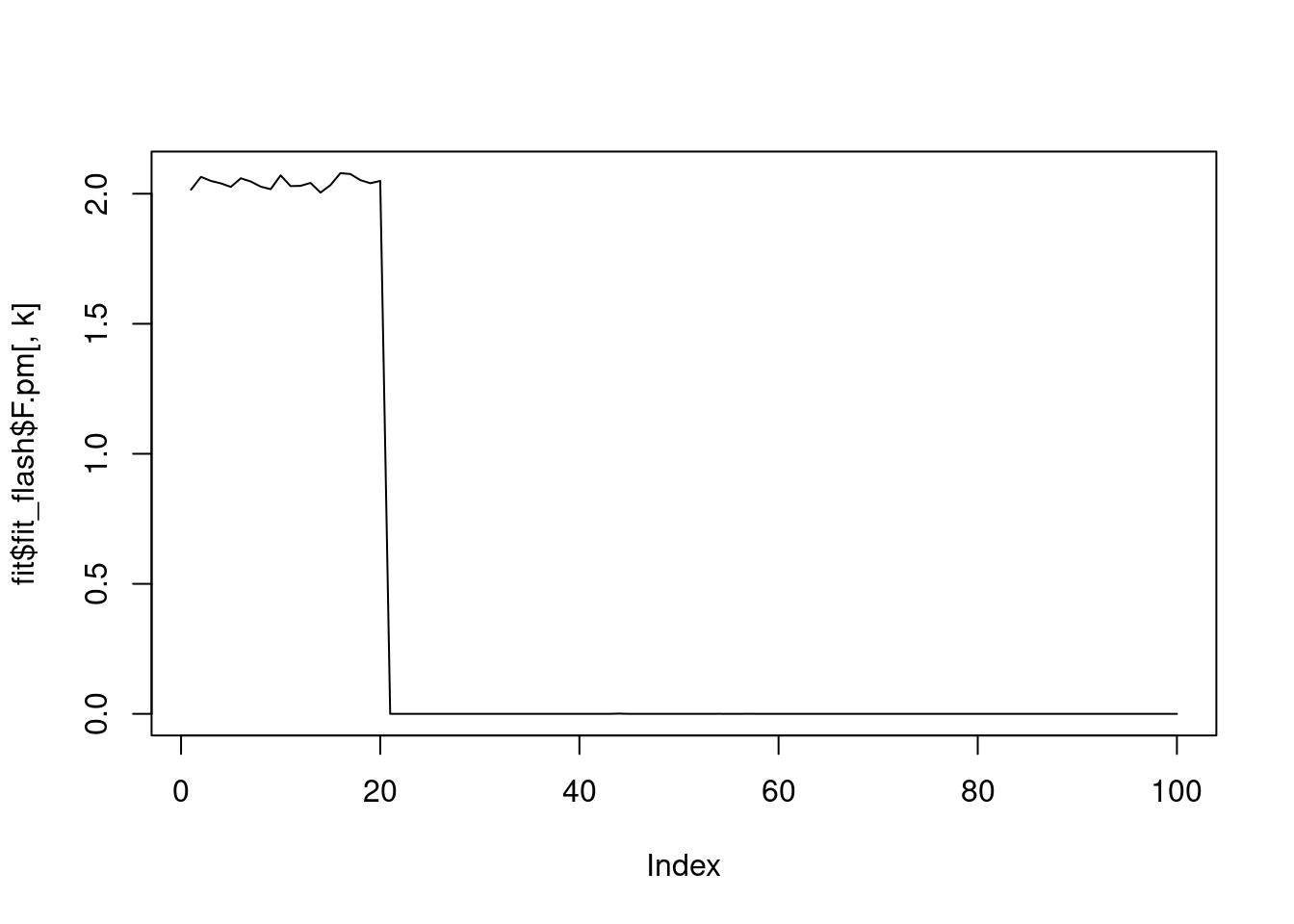
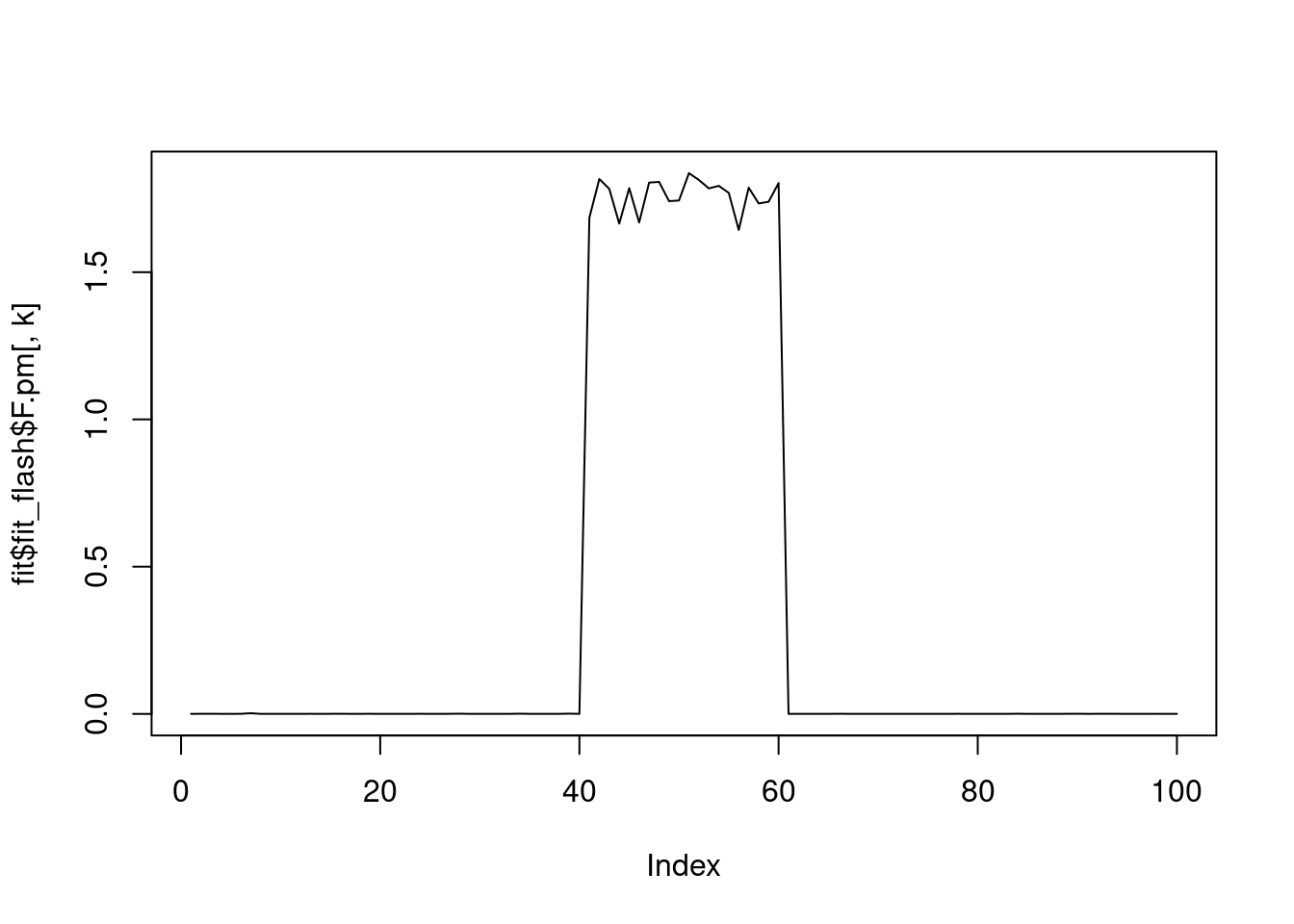
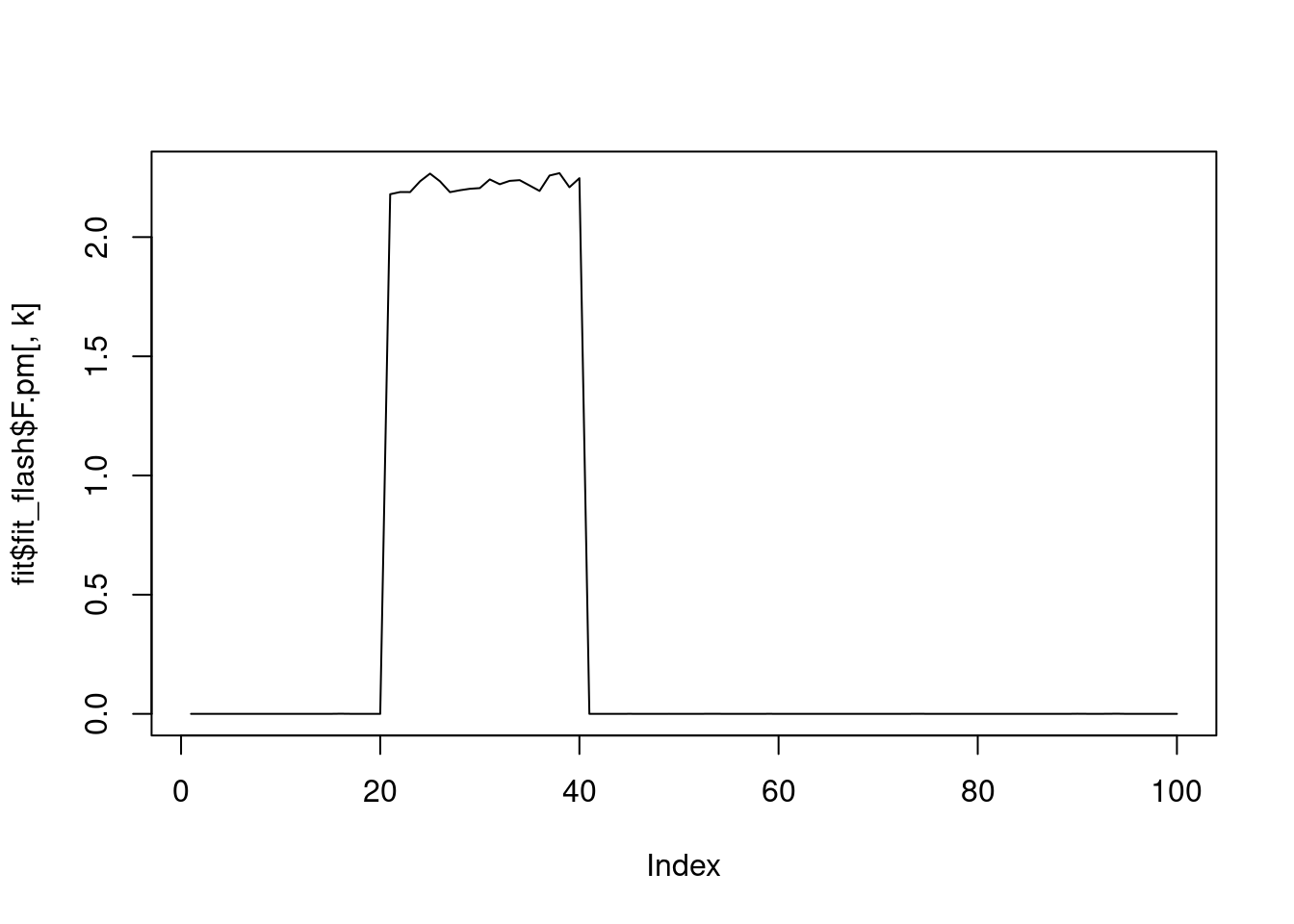
fit$elbo[1] -226205.7plot(fit$fit_flash$pve)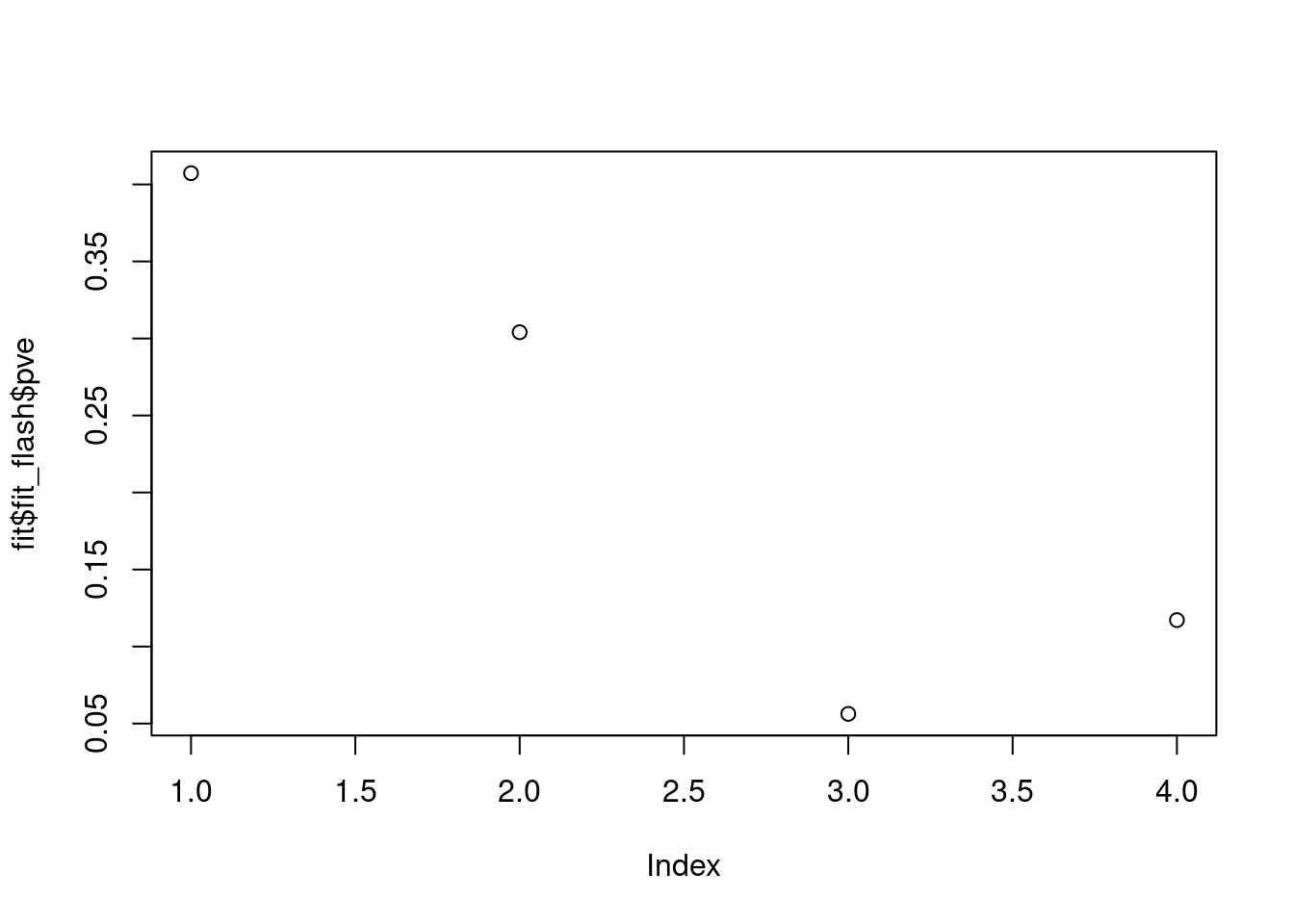
fit$run_timeTime difference of 2.056673 minsunlist(lapply(fit$run_time_break_down,mean)) run_time_vga_init run_time_flash_init
0.262950659 3.614609241
run_time_vga run_time_flash_init_factor
0.030562154 0.139583826
run_time_flash_greedy run_time_flash_backfitting
0.566023827 3.514735298
run_time_flash_nullcheck
0.002779348
sessionInfo()R version 4.2.2 Patched (2022-11-10 r83330)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 22.04.1 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] stm_1.3.5 workflowr_1.7.0
loaded via a namespace (and not attached):
[1] Rtsne_0.16 ebpm_0.0.1.3 colorspace_2.0-3
[4] smashr_1.3-6 ellipsis_0.3.2 mr.ash_0.1-87
[7] rprojroot_2.0.3 fastTopics_0.6-142 fs_1.5.2
[10] rstudioapi_0.14 MatrixModels_0.5-1 ggrepel_0.9.2
[13] fansi_1.0.3 codetools_0.2-19 splines_4.2.2
[16] cachem_1.0.6 knitr_1.41 jsonlite_1.8.4
[19] nloptr_2.0.3 mcmc_0.9-7 ashr_2.2-54
[22] smashrgen_1.1.5 uwot_0.1.14 compiler_4.2.2
[25] httr_1.4.4 RcppZiggurat_0.1.6 Matrix_1.5-3
[28] fastmap_1.1.0 lazyeval_0.2.2 cli_3.4.1
[31] later_1.3.0 htmltools_0.5.4 quantreg_5.94
[34] prettyunits_1.1.1 tools_4.2.2 coda_0.19-4
[37] gtable_0.3.1 glue_1.6.2 dplyr_1.0.10
[40] Rcpp_1.0.9 softImpute_1.4-1 jquerylib_0.1.4
[43] vctrs_0.5.1 iterators_1.0.14 wavethresh_4.7.2
[46] xfun_0.35 stringr_1.5.0 ps_1.7.2
[49] trust_0.1-8 lifecycle_1.0.3 irlba_2.3.5.1
[52] NNLM_0.4.4 getPass_0.2-2 MASS_7.3-58.2
[55] scales_1.2.1 hms_1.1.2 promises_1.2.0.1
[58] parallel_4.2.2 SparseM_1.81 yaml_2.3.6
[61] pbapply_1.6-0 ggplot2_3.4.0 sass_0.4.4
[64] stringi_1.7.8 SQUAREM_2021.1 highr_0.9
[67] deconvolveR_1.2-1 foreach_1.5.2 caTools_1.18.2
[70] truncnorm_1.0-8 shape_1.4.6 horseshoe_0.2.0
[73] rlang_1.0.6 pkgconfig_2.0.3 matrixStats_0.63.0
[76] bitops_1.0-7 ebnm_1.0-11 evaluate_0.19
[79] lattice_0.20-45 invgamma_1.1 purrr_0.3.5
[82] htmlwidgets_1.6.0 Rfast_2.0.6 cowplot_1.1.1
[85] processx_3.8.0 tidyselect_1.2.0 magrittr_2.0.3
[88] R6_2.5.1 generics_0.1.3 pillar_1.8.1
[91] whisker_0.4.1 withr_2.5.0 survival_3.5-0
[94] mixsqp_0.3-48 tibble_3.1.8 crayon_1.5.2
[97] utf8_1.2.2 plotly_4.10.1 rmarkdown_2.19
[100] progress_1.2.2 grid_4.2.2 data.table_1.14.6
[103] callr_3.7.3 git2r_0.30.1 digest_0.6.31
[106] vebpm_0.4.0 tidyr_1.2.1 httpuv_1.6.7
[109] MCMCpack_1.6-3 RcppParallel_5.1.5 munsell_0.5.0
[112] glmnet_4.1-6 viridisLite_0.4.1 flashier_0.2.34
[115] bslib_0.4.2 quadprog_1.5-8